SpinLaunch proposes to launch spacecraft by spinning them up in a centrifuge (prototype shown), then flinging them into the heavens.COURTESY OF SPINLAUNCH

It’s obvious, but I'll say it: Rockets are cool. Sending stuff into space with a chemical reaction is just stupid-awesome. But clearly, we can't keep using chemical rockets to put satellites in orbit. They're too expensive, and the fuel is heavy—which means you need even more fuel to carry the fuel.

So I’m excited about this new proposed launch system, the SpinLaunch. The basic idea is to physically throw a missile off the planet, in much the same way our ancestors hurled rocks with a leather sling. In this case, a giant centrifuge would spin the craft around in a vacuum to build up insane speed, then open a door and release it into the sky.

But the physicist in me also can’t help being a little skeptical. The challenges here—like air drag, for starters—seem enormous. I’m not saying this thing won’t work, but I want to crunch the numbers myself to see what’s involved. Come on, let's take it for a spin!

Acceleration Sensation

Before I get to the calculations, let's look at the details of the system and the physics involved. Here's what I know about SpinLaunch from current specs:

Launcher spins in a circle with a diameter of 100 meters.
Payload mass of 100 kilograms, plus maybe another 100 kg for the spacecraft (I assume this is just a small prototype)
Rotation speed at launch of 450 revolutions per minute
Launch speed of 7,500 kilometers per hour (4,660 mph)
Spin-up time of 1.5 hours
Launch angle at 35 degrees

Just to be clear, it’s still a rocket. Once the craft reaches the outer atmosphere, at an altitude of about 60 kilometers, it uses a small rocket engine to push it the rest of the way.

Now for some physics. There's a bunch of stuff here, so I'll just go over the key ideas. I'll start with objects spinning in a circle. Suppose I take a ball on a string and swing it around in a horizontal plane. As viewed from the top, it would look like this: 

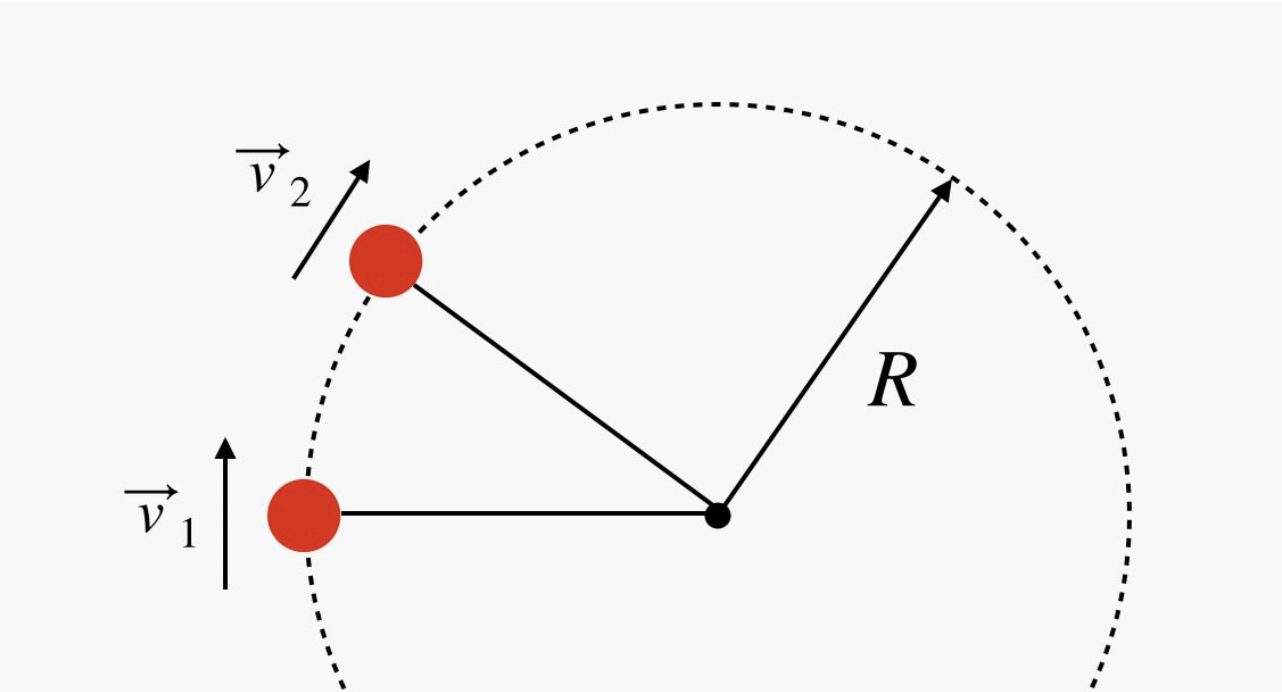
ILLUSTRATION: RHETT ALLAIN

This shows the ball at two different points. As you can see from the arrows, even if the ball is moving at a constant speed, it’s constantly changing direction. By definition, that means the velocity of the ball is changing—velocity is a vector with both speed and direction—which, in turn, means it’s accelerating. This comes straight from the vector definition of acceleration: 

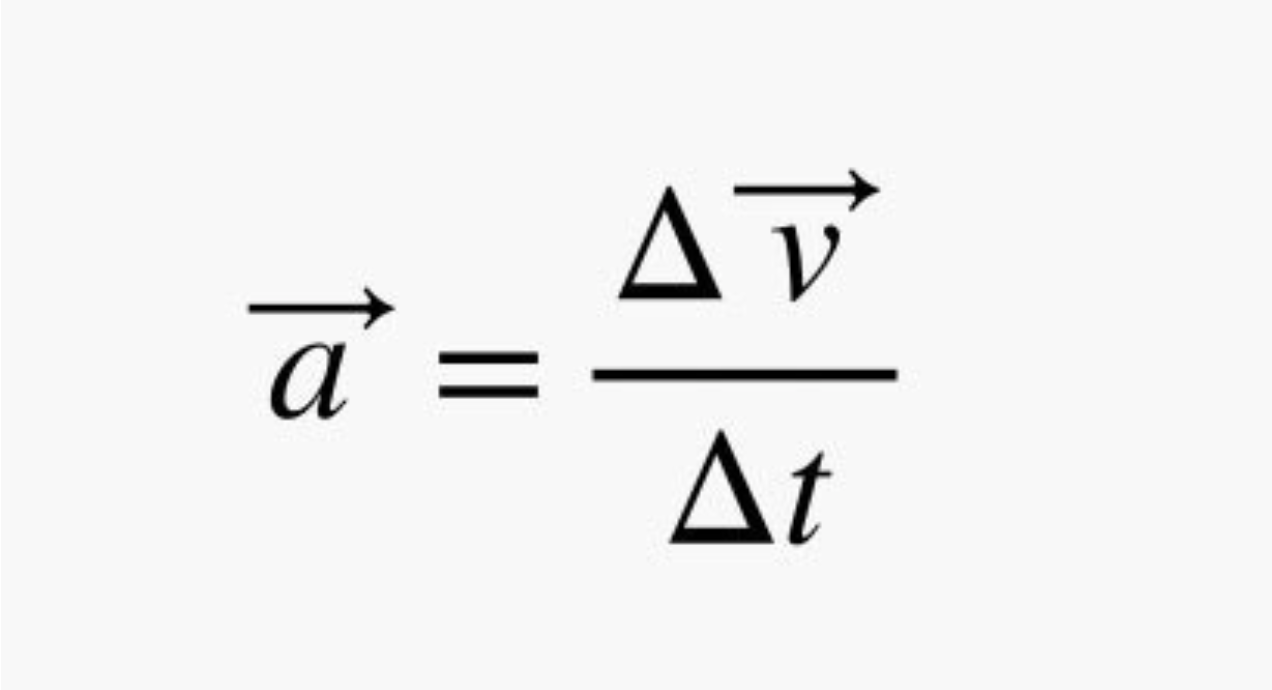
ILLUSTRATION: RHETT ALLAIN

For the special case of circular motion, the magnitude of this acceleration would be:

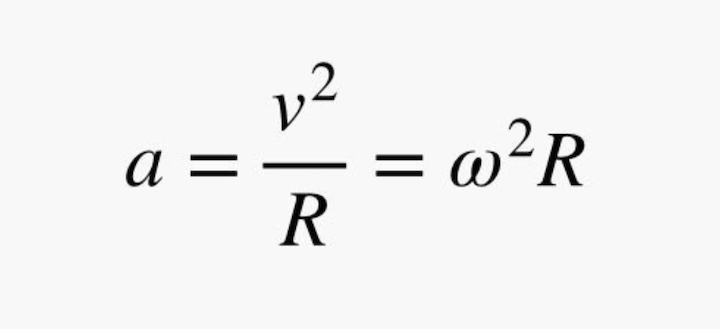
ILLUSTRATION: RHETT ALLAIN

Here, v (without the arrow over it) is the magnitude of the ball’s linear velocity, and R is the radius of the circle. This means that going faster results in a higher acceleration, and making the circle bigger reduces the acceleration.

As shown above, you can also write that in terms of angular velocity (ω) instead of linear velocity. But it's really the same thing, since the speed equals the product of the angular velocity and the radius (if ω is in units of radians per second). Oh, the direction of this acceleration is toward the center of the circle.

Using this, you can calculate the acceleration of the payload as it approaches launch speed. The result, in terms of g forces, is mind-boggling—OVER 9,000, as the kids say. In fact it’s more than 10,000 g’s. For comparison, humans can’t handle more than 10 g’s for any extended period.

Obviously this won’t work for carrying astronauts or space tourists (and SpinLaunch is clear that it’s not meant to). If you got in this thing, you’d be squashed like a bug on a windshield before you took off. I suspect it might be tricky for certain kinds of cargo as well—things with external structures like solar arrays could be too fragile, so satellite designers would need to take the rigors of the launch into account.

How Much Force Does It Require?

But it's not just the acceleration that creates challenges, it's also the force needed to pull the spacecraft around in a circle. The magnitude of this force can be calculated using the following force-motion relationship (often called Newton's Second Law).

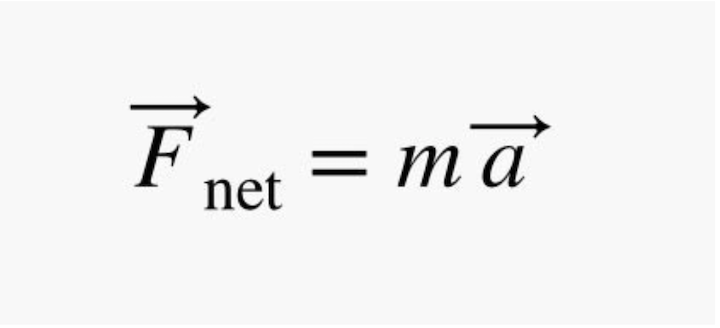
ILLUSTRATION: RHETT ALLAIN

So let's use the numbers from SpinLaunch and calculate the force needed to whip a spacecraft up to speed. I’m doing this in a Python script, linked below, so you can actually go in and change the assumptions to see how they affect the results—click the pencil icon to see the code. Here's what I get:

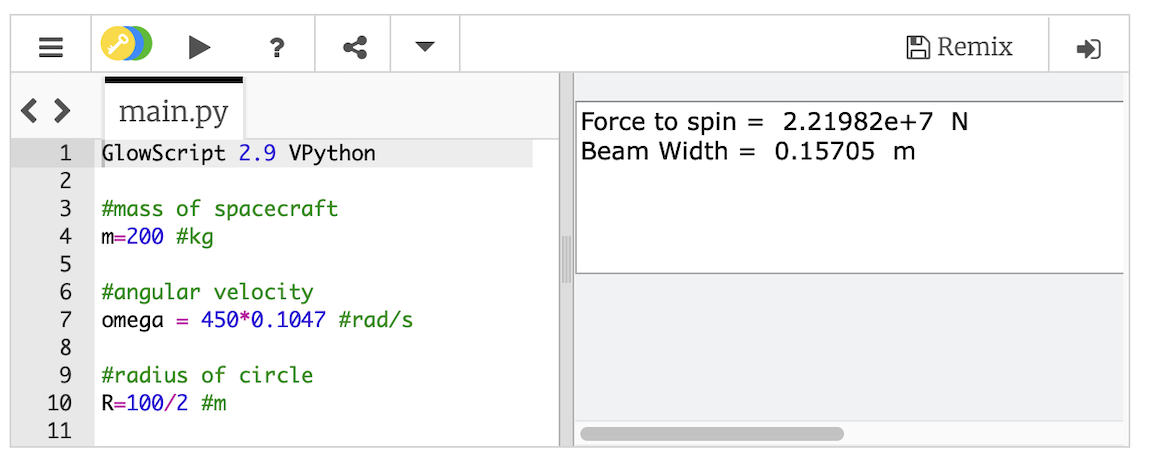
Yup. That's a force of 22 MILLION newtons (or, for you imperials, about 5 million pounds). That's almost as much force as you'd need to hold up a Saturn V rocket. Just imagine using some type of metal bar (like a giant spoke on a wheel) to withstand that kind of force. It almost seems like you couldn't do it.

But after a quick search, I found that a titanium alloy has an ultimate tensile strength of 900 MPa. With that, I can calculate the width of a beam with a square cross section that can support this force. Actually, as you can see above, it isn't bad—just 15 centimeters. That's doable.

What about the power? Power is the rate that you do work (with respect to time). In this case, the work done is the increase in kinetic energy of the spacecraft, where kinetic energy is defined as:

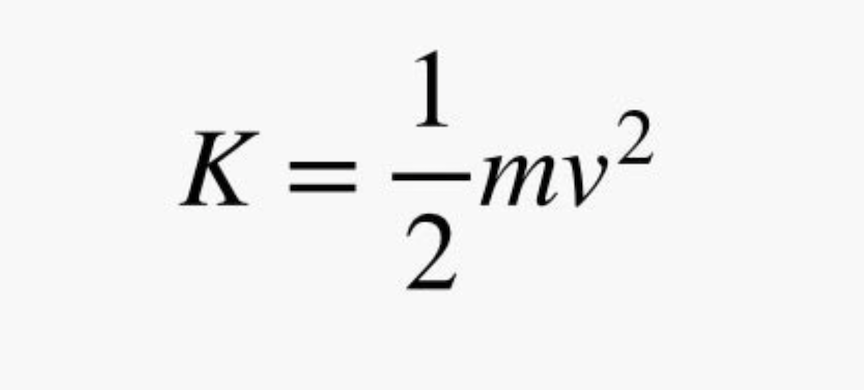
ILLUSTRATION: RHETT ALLAIN

With this change in kinetic energy and a time of 1.5 hours, I get an average power of 103 kilowatts. That's pretty high, but not crazy high for something like this.

Can It Reach Orbit?

So far everything seems legit. I mean, you shouldn't build this in your backyard or anything, but from an engineering standpoint it looks possible. But can a system like this actually put a payload in orbit? For that we need to review orbital motion. (This older post also gives a pretty good overview on the topic.)

Let's say you want to get this payload to low earth orbit (LEO), like where the International Space Station orbits. You have to do two things: First, you need to get up to orbital height, about 400 kilometers above the surface of the Earth. Second, you have to go fast—real fast. Otherwise you just fall back down.

For LEO, that means the spacecraft needs a final speed of 7,666 meters per second (17,148 mph). Clearly, this spinning launch isn't going to get the thing all the way into orbit, but it will give it a nice boost.

But wait. There’s another issue—air drag. As soon as this vehicle is launched from the spinner thing, it enters the atmosphere. As it moves through the air, the air pushes back on the craft with a force that depends on its speed (v). We call this the air drag force. It's the thing you feel when you put your hand out of a moving car window. This force also depends on the density of the air (ρ), the shape of the object (C), and its cross-sectional area as viewed from the front (A). The magnitude of this force can be modeled (in many but not all) cases as the following:

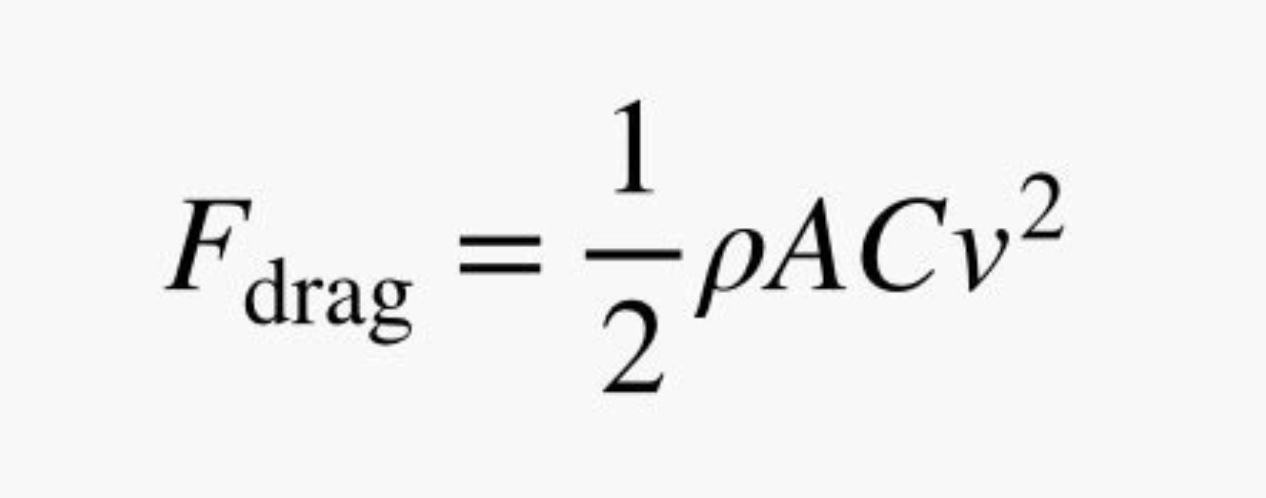
ILLUSTRATION: RHETT ALLAIN

I want to use this and calculate the acceleration of the craft right after it leaves the launcher. This acceleration will be due to the drag force—and since it pushes in a direction opposite to its motion, it will make it slow down. (To a physicist, any change in velocity, positive or negative, is acceleration.)

Of course, I’m going to need to make a few estimates for the size, shape, and mass of the craft. The most difficult estimate will be the drag coefficient. Stuff gets weird at super high speeds. I'm just going to go with the lowest reasonable value of around 0.1. Again, here are all my values, so you can try different assumptions:

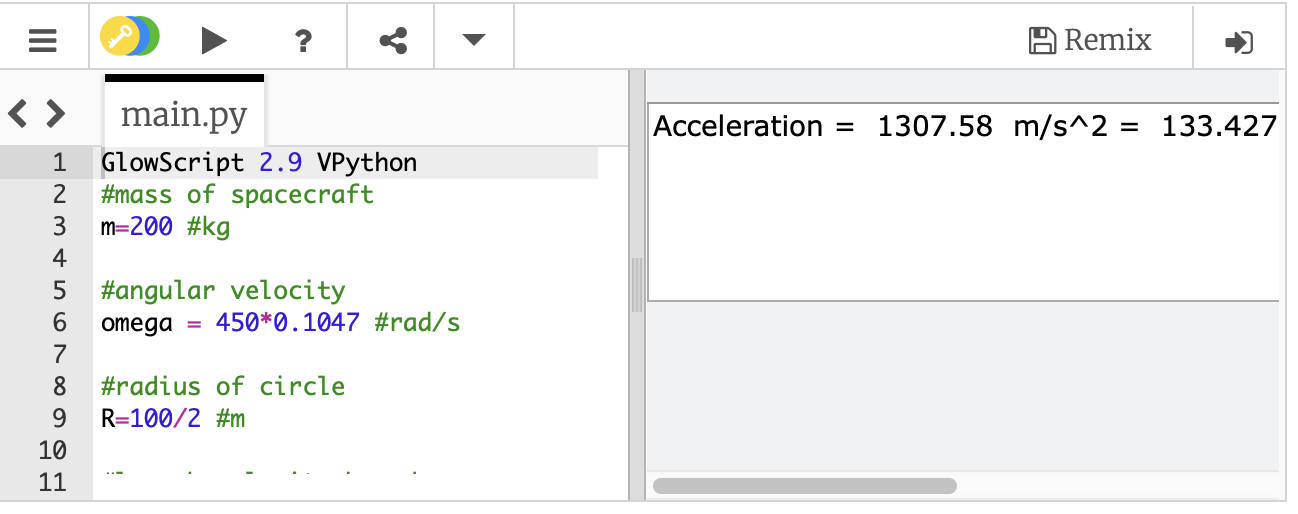
That means that when the craft leaves the launcher, it's going to start slowing down—real fast. If you were inside, the effect of hitting the air would likely kill you. But don't worry, you were already dead from the spinning part. But with this high acceleration, the craft will slow down quite a bit. It's really going to need that rocket engine to give it a boost.

OK, I'm still excited to see this thing work! In the meantime, here are some physics homework questions for you.

• Suppose Earth had no atmosphere. How high would the spacecraft get from just the spin launch if it was shot straight up? What if it was launched at a 35-degree angle? Do you have to take into account the curvature of the planet?
• Calculate the total amount of energy needed to get this craft into LEO. What percent of this value does the spinner provide?
• Again, ignore air resistance. How fast would this thing have to spin to get the craft all the way to LEO without a rocket boost? If it was still using 100 kilowatts of power, how long would it take to spin up? What kind of acceleration would the payload have during the spin?
• What about a bigger spinner? What would happen if you increased the diameter from 100 m to 200 m? Would this make it better? Is it possible to make it big enough such that the acceleration wouldn't kill a human?
• Model the motion of the craft after it is released, including a calculation of drag force. 

By Rhett Allain, Wired

         Rhett Allain is an Associate Professor of Physics at Southeastern Louisiana University. He enjoys teaching and talking about physics. Sometimes he takes things            
        apart and can't put them back together.